Task 1: Learning about Pythagoras
In your class notebook, date the next clean page and label it, “Pythagorean Theorem WebQuest”. Organize your notes for each task under headings such as, "Task ___".
Visit the websites below to gain a better understanding of who Pythagoras was and what he brought to the mathematical community other than the Pythagorean Theorem. Write down at least 5 new facts that you gather in your research. Focus on the mathematical aspects of his life.
http://www.historyforkids.org/learn/greeks/science/math/pythagoras.htm
http://www.notablebiographies.com/Pu-Ro/Pythagoras.html
http://www.mathopenref.com/pythagoras.html
Visit the websites below to gain a better understanding of who Pythagoras was and what he brought to the mathematical community other than the Pythagorean Theorem. Write down at least 5 new facts that you gather in your research. Focus on the mathematical aspects of his life.
http://www.historyforkids.org/learn/greeks/science/math/pythagoras.htm
http://www.notablebiographies.com/Pu-Ro/Pythagoras.html
http://www.mathopenref.com/pythagoras.html
Task 2: Explore the proofs
Read about and try out a few interactive proofs of the Pythagorean Theorem at these websites. For each site, record in your notebook (under "Task 2") the main steps that were followed to do the proof. Also, include the author of the proof if it is attributed to any one person. (Note: I don’t want you to write down every step, just a sentence or two that describes the method.)
#1) http://math.ucr.edu/~jdp/Relativity/Pythagorus.html
#2) http://www.mathsisfun.com/geometry/pythagorean-theorem-proof.html
#3) http://www.pbs.org/wgbh/nova/proof/puzzle/theorem.html
#4) http://www.math.hmc.edu/funfacts/ffiles/10007.2.shtml
#5) Scroll down to “Garfield’s Proof” in the following: http://jwilson.coe.uga.edu/EMT668/emt668.student.folders/HeadAngela/essay1/Pythagorean.html
#6) For this proof, access the document below. You will need to use graph paper to follow along in the proof. Complete the accompanying questions in your notebook.
#1) http://math.ucr.edu/~jdp/Relativity/Pythagorus.html
#2) http://www.mathsisfun.com/geometry/pythagorean-theorem-proof.html
#3) http://www.pbs.org/wgbh/nova/proof/puzzle/theorem.html
#4) http://www.math.hmc.edu/funfacts/ffiles/10007.2.shtml
#5) Scroll down to “Garfield’s Proof” in the following: http://jwilson.coe.uga.edu/EMT668/emt668.student.folders/HeadAngela/essay1/Pythagorean.html
#6) For this proof, access the document below. You will need to use graph paper to follow along in the proof. Complete the accompanying questions in your notebook.
| process_task_2.6.pdf | |
| File Size: | 96 kb |
| File Type: | |
Task 3: Apply the theorem
Label a section in your notebook, “Task 3.” Access the “baseball” and “ladders” examples on the website below, reading through the problem, sketching a figure of what is happening, and solving the problem using the Pythagorean Theorem. Each site has tips to help you get started and a place to check your answer.
http://www.pbs.org/wgbh/nova/proof/puzzle/use.html
http://www.pbs.org/wgbh/nova/proof/puzzle/use.html
Task 4: How far can you see?
Imagine that you’re standing on an ocean beach looking out across the water. The deep blue sky is clearer than you’ve ever seen it, and it seems as though you can see forever! Well, you know that isn’t really possible on Earth. The extent of your vision is limited by Earth’s curvature. You can see to the horizon—and perhaps slightly beyond.
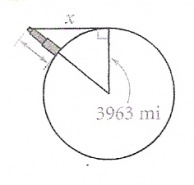
Choose one of the structures on the websites below. Find one that you can see some sort of image of, as well as it’s height in feet. Imagine climbing to the very top to get a good view of the horizon. Assume that Earth is spherical and has a radius of 3963 mi. Also assume that you see a smooth horizon such as that of an ocean or desert. Find the distance from the top of the structure to the horizon. (Hint: Convert your building’s height into a fraction of a mile, then create a picture such as the one below to show and use the Pythagorean Theorem.
http://www.tallestskyscrapers.info/images/tallest-buildings.jpg
http://architecture.about.com/library/bltall.htm
First, sketch and complete your work under "Task 4" in your notebook. Show me your work when you are finished and pick up materials to display your finished work for this task on a poster. This project is to be displayed neatly on posterboard according to the rubric under “Evaluation.” It will be counted as a quiz grade.
Choose one of the structures on the websites below. Find one that you can see some sort of image of, as well as it’s height in feet. Imagine climbing to the very top to get a good view of the horizon. Assume that Earth is spherical and has a radius of 3963 mi. Also assume that you see a smooth horizon such as that of an ocean or desert. Find the distance from the top of the structure to the horizon. (Hint: Convert your building’s height into a fraction of a mile, then create a picture such as the one below to show and use the Pythagorean Theorem.
http://www.tallestskyscrapers.info/images/tallest-buildings.jpg
http://architecture.about.com/library/bltall.htm
First, sketch and complete your work under "Task 4" in your notebook. Show me your work when you are finished and pick up materials to display your finished work for this task on a poster. This project is to be displayed neatly on posterboard according to the rubric under “Evaluation.” It will be counted as a quiz grade.